2. Primeros pasos: trabajando con un sistema de coordenadas

Ya tenemos seleccionada la zona sobre la que vamos a trabajar? Tened en cuenta que solo podemos trabajar con áreas rectangulares. Una vez seleccionado un rectángulo de mapa, es básico determinar las coordenadas que lo determinan.

Es importante tener claro con que sistema de coordenadas vamos a trabajar. Un sistema de coordenadas se determina mediante una Proyección (por ejemplo UTM) y un datum (pe European Datum). En mi caso, tengo mapas del Ejército, a escala 1:50000, que usan proyección UTM y datum europeo. El sistema de coordenadas del Ejército se basa en una rejilla cuadriculada, con cuadrados de 1km de lado. El espacio se organiza en cuadrados de 200km x 200km. Cada cuadrado de 200 x 200 Km se divide en cuatro cuadrantes de 100km x 100km, que se llaman AF, BF, CF y DF.

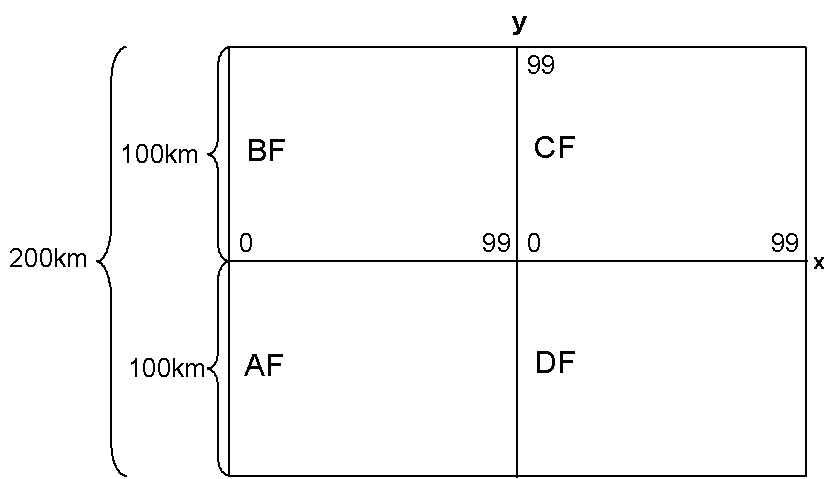
En cada cuadrante, los kilómetros (la cuadrícula) se numera de 0 a 99, de izda a dcha (Oeste a Este) y de abajo arriba (de Sur a Norte). La información sobre los códigos de zona y cuadrante de un mapa topográfico se puede consultar en el propio mapa. En los mapas del Servicio Geográfico Militar esta información viene en una tabla al dorso, que explica también como obtener las coordenadas de un puntodel mapa. Como ejemplo, el mapa de Mora de Ebro proporciona la siguiente información.

Como se ve en la imagen nuestro mapa pertenece a la zona 31T, y cubre parcialmente dos cuadrantes, el BF y el CF

Según este sistema, cada punto del mapa se caracteriza por sus coordenadas X e Y, que van de 0 a 99Km, y aumentan de Oeste a Este y de Sur a Norte respectivamente.

Cada punto se define como [Codigo de Area + Codigo Cuadrante + Coord. X + Coor. Y]

En mi caso, toda la zona de interés pertenece a la zona 31 T y al cuadrante BF, por lo tanto los puntos tienen la estructura siguiente

[31 T CF Coord. X Coor. Y]

Podemos representar la X y la Y en km de 0 a 99, o en metros, de 0 a 99000. Como el Global Mapper mide en metros, a partir de ahora daremos la representación en metros.

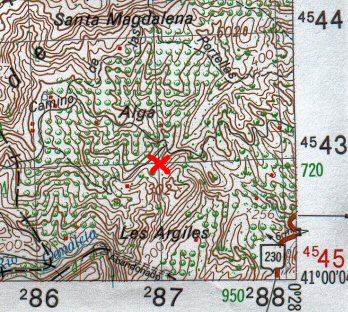En este ejemplo, el punto señalado con aspa roja tiene las coordenadas siguientes: x = 87km = 87000m y= 43km = 43000m (Se usan sólo los números grandes, los pequeños, como el 2 y el 45, son de la proyección UTM, que luego comentaremos) La zona es 31 T y el cuadrante es el BF. Por lo tanto nuestro punto es: 31 T BF 87000 43000

En este otro ejemplo, con aspa azul se señala un punto que se halla aproximadamente en las coordenadas: 31 T BF 87500 43500 Sabiendo que la rejilla marca cuadrados de 100 metros, la mitad son 500 metros. Midiendo con regla sobre papel se puede precisar bastante, y sino usando una regleta con un editor de imagen sobre el mapa escaneado*.

*Nota: puede facilitar las cosas el escanear la imagen haciendo que su resolución (pixels/cm o pixels/pulgada) tenga una equivalencia directa con el tamaño de la rejilla de vuestro mapa. Pe, en los mapas 1:50000 1cm=500m. Si usais una resolución de 100 puntos por centímetro, sabeis que 1Km real equivalen a 200 pixels en vuestra imagen, y cualquier editor de imágenes os dará las coordenadas de un punto cualquiera de la imagen. Si tenemos la imagen con otra resolución, siempre podemos cambiarla mediante un editor de imágenes.

Para delimitar un rectángulo, necesitamos establecer 2 puntos. Por la forma de trabajar del software que utilizaremos después, nos interesa usar 2 vértices del rectángulo, el superior izquierda y el inferior derecha, que se corresponden con las direcciones NO y SE.

Como ejemplo, seleccionamos un zona del Ebro en torno al Barranco Negre, y la delimitamos por los 2 puntos siguientes:

NO(aspa roja): 31 T BF 96000 45000
SE(aspa azul): 31 T BF 98000 43000

Para trabajar con más comodidad aquí se muestra una imagen que cubre una zona algo mayor, aunque se supone que estamos trabajamos con el cuadrado exacto (más tarde veremos un método en el que esa cuestión no es relevante, pues nos permitirá sincronizar un rectángulo arbitraro con el área de terreno equivalente en el MET).